Pola Bilangan
Jika anggota-anggota suatu himpunan diurutkan menurut suatu aturan tertentu maka akan membentuk suatu barisan bilangan. Perhatikan barisan bilangan berikut ini:
1, 2, 3, 5, 8, 13, 21, 34,…
Urutan bilangan-bilangan tersebut adalah sebagai berikut:
urutan ke-1 adalah 1
urutan ke-2 adalah 2
urutan ke-3 adalah 3
urutan ke-4 adalah 5
urutan ke-5 adalah 13
urutan ke-6 adalah 21
urutan ke-7 adalah 34
urutan ke-2 adalah 2
urutan ke-3 adalah 3
urutan ke-4 adalah 5
urutan ke-5 adalah 13
urutan ke-6 adalah 21
urutan ke-7 adalah 34
Ternyata nomor urut bilangan-bilangan tersebut merupakan bilangan asli. Oleh karena itu barisan dapat didefinisikan sebagai fungsi dari bilangan asli atau fungsi yang domainnya adalah bilangan asli.
Anggota-anggota barisan bilangan disebut suku dan dinotasikan dengan U. Keterkaitan bilangan asli dengan anggota-anggota suatu barisan dapat digambarkan sebagai berikut :
Un = f(n) artinya bahwa suku-suku barisan bilangan merupakan fungsi dari bilangan asli.
Dengan demikian barisan bilangan dapat dinyatakan dengan : U1, U2, U3, U4, ..., Un.
Dengan demikian barisan bilangan dapat dinyatakan dengan : U1, U2, U3, U4, ..., Un.
Barisan Bilangan
Diketahui suatu barisan bilangan : 1, 4, 9, 16, . Bagaimana pola barisan bilangan tersebut?
Nampak bahwa :
suku ke-1 = U1 = 1
suku ke-2 = U2 = 4
suku ke-3 = U3 = 9
suku ke-4 = U4 = 16
suku ke-2 = U2 = 4
suku ke-3 = U3 = 9
suku ke-4 = U4 = 16
Jika digambarkan dengan diagram panah, maka diperoleh pola sebagai berikut :
Hubungan setiap anggota himpunan A ke anggota himpunan B dapat dideskripsikan sebagai kuadrat dari
Sehingga dapat dikatakan bahwa barisan tersebut mempunyai suku ke-n
Diketahui suatu barisan bilangan : 2, 5, 8, 11,. Bagaimana pola barisan bilangan tersebut?
Jika anggota-anggota barisan bilangan tersebut dihubungkan dengan angota domainnya (bilangan asli).
Notasi Sigma
Notasi sigma adalah sebuah tanda yang digunakan untuk menuliskan penjumlahan secara singkat. Notasi sigma, ditulis dengan 
Secara umum, notasi sigma didefinisikan sebagai berikut :

Dimana:
Sifat-sifat notasi sigma:






Secara umum, notasi sigma didefinisikan sebagai berikut :

Dimana:
i adalah indeks penjumlahan
n adalah batas bawah penjumlahan
n adalah batas atas penjumlahan
Sifat-sifat notasi sigma:





1. Barisan Aritmatika
Bentuk umum:
U1, U2, U3,………. Un
Rumus:
beda -> b = Un - Un-1
suku ke-n barisan aritmatika:
Un = a+(n-1)b
Un = Suku ke-n
a = Suku pertama = U1
b = beda
Contoh soal:
1. Diketahui barisan 6, 9, 12,..
Tentukan: a. Beda
b. Suku ke 50
Jawab:
a. b = Un -Un-1 =9-6 = 3
b. S50 = a+(n-1)b
= 6+(50-1) 3
= 6+(49) 3
= 153
Jadi, suku ke-50 adalah 153.
2. Diketahui barisan aritmatika dengan U = 2 dan U = 14.
Tentukan: a. Nilai suku pertama dan bedanya b. Suku ke-25
Deret aritmatika
Bentuk umum:
U1,u2,u3……un
Rumus:
Jumlah n suku pertama:
Sn = n/2 (a + Un ) atau Sn = n/2 {2a + (n - 1)b atau Un = Sn - Sn - 1
Contoh soal:
Hitunglah jumlah 50 suku pertama dari deret 2 + 4 + 6 + 8 + …….
Jawab:
2 + 4 + 6 + 8 + …… U50
a = 2, b = 2, n = 50
Sn = n/2 { 2a + (n - 1)b}
S50 = 50/2 {2(2) + (50 - 1)2}
= 25 {4 + (49)2}
= 25 {4 + 98}
= 25 (102)
= 2550
2. Barisan Geometri
Barisan bilangan U1,U2,U3,…… Un disebut dengan barisan geometri, apabila punya yang namanya rasio (r).
r = U2/U1 = U3/U2 = U4/U3 = Un/Un-1
Contoh soal:
- Tentukan rasio ke 8 dari barisan 2,4,8,16,…
a = 2
r = 4/2
= 2
Un = arn-1
U10 = 2 . 210-1
= 2 . 29
= 2 . 512
= 1024
Deret geometri
Bentuk umum
U1 + U2 + U3 +…… + Un
a + ar + ar2 +…….. + arn-1
Rumus jumlah n suku deret geometri:
Sn = a (1 - rn)/1 - r jika r < 1
Dan
Sn = a (rn - 1)/r - 1 jika r > 1
Contoh soal:
Hitunglah jumlah 8 suku dari deret 2 + 4 + 8 +…..
Jawab:
2 + 4 + 8 +….
a = 2
r = 2 berarti harus memakai yang r > 1
maka:
Sn = a (rn - 1)/r-1
S8 = 2 ( 28 - 1)/ 2-1
= 2 (256 - 1)/2-1
= 2 (255)
= 510












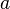






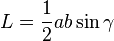








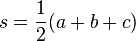
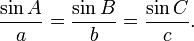
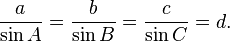

 adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut
adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut